The previous article mentioned that TSP is a common problem in the logistics industry (in fact, it’s not limited to logistics; factory production line scheduling can also be a TSP-type problem). Since Google Maps already has an API, why use our service?
Because the Google Maps API is too different from what the frontline requires.
1. Some goods are time-sensitive
Think about it: it’s impossible for every shipment a logistics fleet delivers to meet delivery deadlines, especially with the current surge in e-commerce. Buyers place orders on platforms, goods are picked and sorted at warehouses, and then transported to local locations. That last mile only has about eight hours. If a driver has to deliver to 100 addresses today, and 40 of them have delivery deadlines, Google Maps won’t cut it.
2. Truck capacity is limited
Think about it, cargo comes in all sizes, and trucks come in all sizes. Google Maps can only tell you how to efficiently deliver cargo, but you have to make sure the cargo can fit on the truck.
3.A logistics fleet won’t just have one vehicle
This is the key point. Unless a fleet consists of only one vehicle, how can it deliver goods? Is there something wrong?! This point is actually related to the digital transformation of logistics fleets, which we will discuss in a separate article in the future.
4.Doesn’t the driver need to rest?
Google maps doesn’t care about this! This is something the logistics fleet has to handle themselves.
In short, TSP is for students to practice in school and let them know what effects mathematics can have in the industry, but there is still a long way to go before we can apply what we have learned at the school level to the front line.
So what is the problem that is more in line with the reality of logistics fleets?
I refer to the Vehicle Routing Problem (VRP). The core question VRP seeks to answer is: What is the optimal set of routes for a fleet of vehicles to deliver goods to a given set of customers? Put another way, suppose a warehouse has K packages to deliver to m different locations, but only n vehicles are available. These vehicles may vary in size or capacity, and each of the K packages may have specific time constraints. The challenge is: How should the K packages be assigned to the nvehicles, and in what delivery sequence should each vehicle operate, so that all deliveries are completed without delay, with the minimum total travel distance, and each vehicle returns to the warehouse?
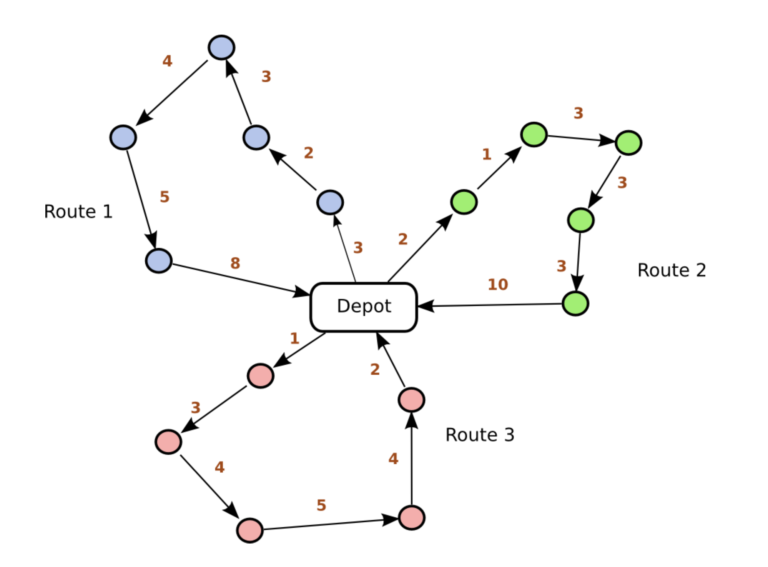
While the above description might seem confusing to most people, mathematicians are able to transform this problem into a mathematical model. Anyone who has actually run a VRP knows it’s significantly more complex than the TSP, attracting considerable research. This has led to numerous different VRP types, tailored to different industries, as shown in the figure below.
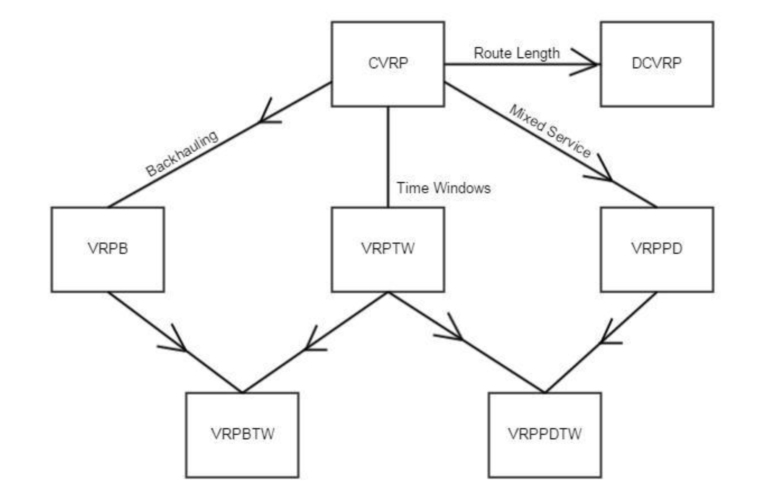
The VRP model is more consistent with the reality of the logistics industry because it describes the scenario of multiple trucks and can be modified into different mathematical models depending on the industry. The following are some common variations:
C: Capacitated This means considering the truck capacity limit (this is super basic!)
TW: Time Window This means considering whether the recipient has specified a time, which is the timeliness mentioned above.
PD: Pick-up Delivery I’ve translated it into pick-up and delivery. This model has many variations, such as reverse logistics or food delivery.
B: Backhaul
MD: Multi-Depot In reality, a company may have more than one warehouse.
So does Google Maps completely fail to meet frontline logistics needs?
This is too harsh. If I were to answer, I would say: it will come at a huge price.
Anyone who has operated VRP must know that when solving the VRP family problem, we must first generate a distance matrix.
In mathematics, a distance matrix is a two-dimensional array in which each element represents the distance between a pair of points. Given N points in Euclidean space, the corresponding distance matrix is an N × Nsymmetric matrix with non-negative real numbers as its elements.
The concept of a distance matrix is similar to that of an adjacency matrix, but with a key difference: an adjacency matrix only indicates whether a pair of elements (nodes) is connected by an edge, without providing information about the actual distance between them. Therefore, a distance matrix can be seen as a weighted version of an adjacency matrix.
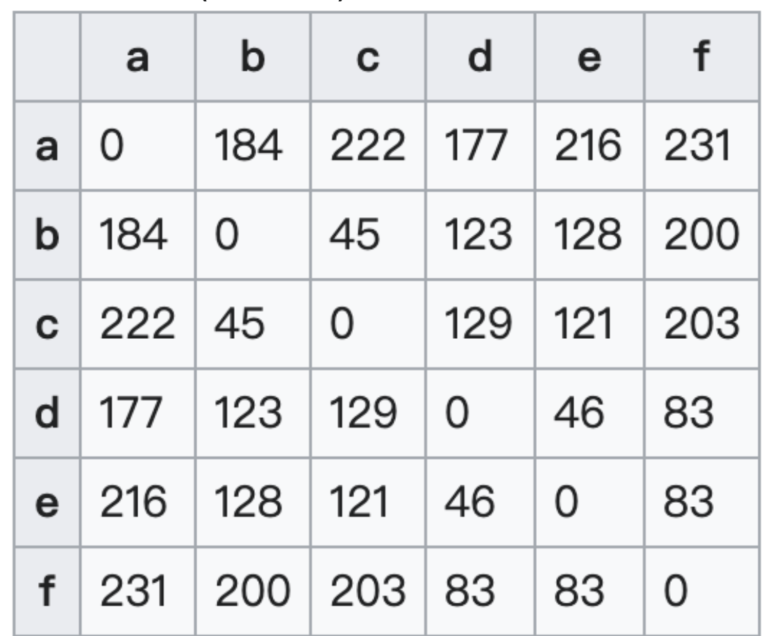
Generating this matrix is extremely costly. For example, in the table above (assuming the logistics company wants to deliver goods from point a to points b, c, d, e, and f), the shortest path distance between points must be calculated 20 times (excluding the diagonal).
When the number of points is small, the computational cost is relatively low. Using the classic Dijkstra algorithm, computing the shortest path between a single origin-destination pair—within a road network roughly the size of Taipei City—takes around 20 milliseconds. Therefore, generating the entire distance matrix (i.e., all pairwise distances) may take only about 400 milliseconds before entering the VRP computation stage. (Here, we are not considering approximations like Manhattan distance for speed-up.)
However, as mentioned earlier, a single 3.5-ton delivery truck might need to visit 100 locations in a day. This results in a distance matrix with 9,900 shortest path computations (i.e., 100×9922100×99), requiring approximately 9,900 × 20ms = 198 seconds before VRP solving can even begin. That’s over 3 minutes spent just on computing distances—long before tackling the actual VRP, which is computationally much more complex.
While Google Maps does offer a Distance Matrix API to handle this step, the cost can be prohibitive. According to their official pricing, each origin-destination distance query costs approximately $0.01 USD.
At the scale shown above, computing a full distance matrix would cost 20 × $0.01 = $2 USD. That might not sound like much—but for a 3.5-ton delivery truck visiting 100 addresses in a day, that’s 9,900 shortest path queries, which adds up to a shocking $99 USD! And keep in mind: this only gives you the distances. It does not include any route optimization. You still have to build your own algorithm to actually solve the VRP!