上篇文提到TSP是一種物流業常會遇到的問題類型(其實不只物流業,工廠的產線 排程也可以是一種TSP類型的問題)。既然google maps已經出了API了,那為什麼要 用我們家的服務?
因為google maps的API跟第一線要的差太多了
1. 有些貨物有時效性
想想,物流車隊要送的貨物裡,不可能每一件貨都沒有時效,尤其現在電商這麼 發達,買家從平台上下單,在倉庫揀貨理貨,運輸到地方的站點,此時最後一哩 只剩下約8小時。假如今天司機大哥要送100個地址,其中有40個地址有時效限制 ,那麼google maps就不行了。
2. 貨車容量是有限的
再想想,貨物有大有小,貨車也有大有小。Google maps只能告訴你一輛車怎麼送 貨才有效率,但是你要自己確定『那些貨能夠被裝上車』
3.物流車隊不會只有一輛車
這才是重點,除非這家車隊只有一輛車,否則只能算一輛車怎麼送貨,這是不 是哪裡搞錯了?!有關這一點其實與物流車隊的數位轉型有關,未來我們會 專文論述。
4.司機不用休息嗎?
Google maps哪管這件事!這是物流車隊自己要處理的。
總而言之,TSP是在學校讓同學練習的,讓同學知道數學可以在業界發揮甚麼 效果,但拿學校等級的東西想要套在第一線,還有一大段路要走。
那麼比較符合物流車隊現實的是什麼問題?
我會說是車輛路線問題(Vehicle Routing Problem, VRP)。VRP要解決的問題是「為了 交付給定的一組客戶,車輛車隊的最佳路線集是什麼?」,換個方式說,某倉庫有K件 貨要送去m個地址,但只有n輛車。這n輛車可能有不同大小,K件貨各有其時效性,請 問:這K件貨和這n輛車的搭配為何?以及每輛車送貨的順序為何?才能夠在不遲到的 前提下,用最少行駛里程送完,並回到倉庫?
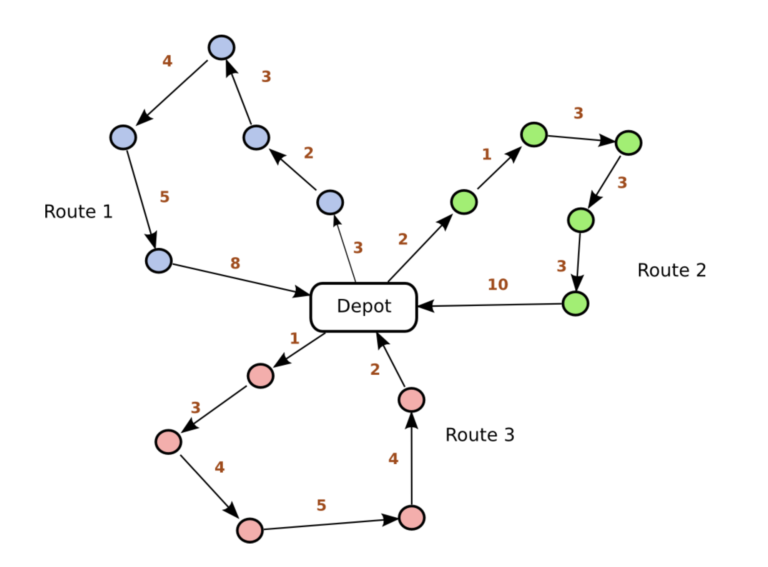
通常一般人看到上述的描述就昏了,但是數學家就能夠把這種問題變成數學模型。 真正有操作過VRP的人一定知道它比TSP複雜多了,也吸引很多學者下去研究 ,也因應業種的不同衍伸出了很多不同的VRP類型,如下圖所示。
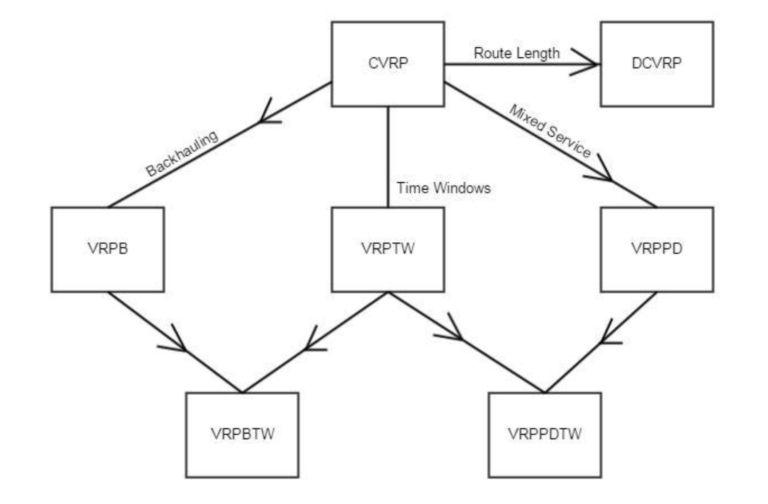
VRP比較符合物流業現實主要是因為這個模型描述了多輛貨車的情境,而且可 以再依業種不同修改成不同的數學模型,以下舉幾個常見的變形:
C: Capacitated 意指要考慮貨車容量限制(這個超基本的對吧!)
TW: Time Window 意指要考慮收貨者有沒有指定時間,也就是前文的時效性。
PD: Pick-up Delivery 我都翻成邊揀邊送。這個形式又有好多變形,像是逆物流, 或是食物快遞。
B: Backhaul 回頭車。
MD: Multi-Depot 現實中一家公司可能不只一個倉庫。
那麼google maps完全無法符合第一線的物流需求嗎?
這樣講也太嚴苛,如果我來回答,我會說:要付出極大代價。
有操作過VRP的人一定知道,在解算VRP家族問題時,我們要先產生距離矩陣。
在數學中, 一個距離矩陣是一個各項元素為點之間距離的矩陣(二維數組)。因此 給定N個歐幾里得空間中的點,其距離矩陣就是一個非負實數作為元素的N×N的對稱 矩陣距離矩陣和鄰接矩陣概念相似,其區別在於後者僅包含元素(點)之間是否有連邊 ,並沒有包含元素(點)之間的連通的距離的訊息。因此,距離矩陣可以看成是鄰接矩陣的加權形式(維基百科)。
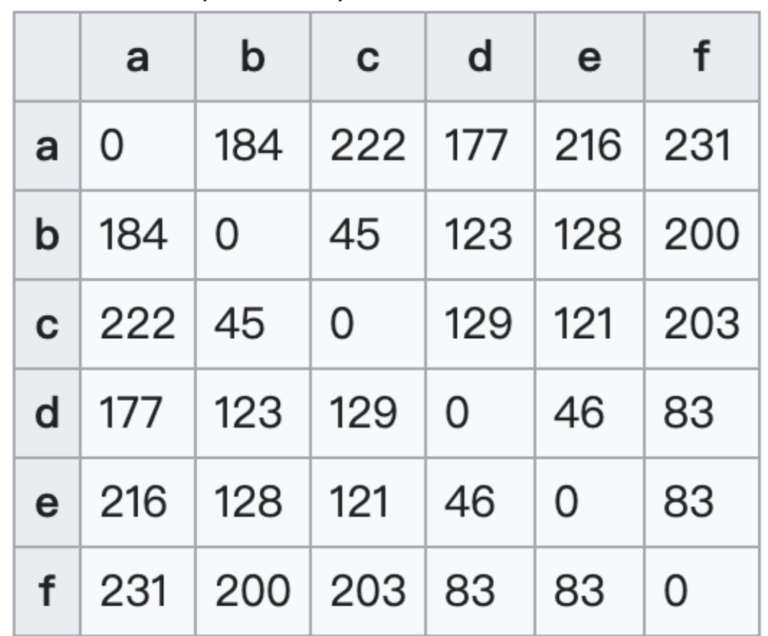
這一個矩陣的產生要花費極大的成本,以上面這張表的例子(可以假設物流公司 要從a點出發去送貨到b,c,d,e,f點),要計算20次點到點的最短路徑距離(扣掉對角線)。
在點數少的時候,計算成本小,以經典的Dijkstra演算時,約台北市大小的路網,一對起訖的最短路徑演算(就是上表的一格)只需20ms,上述的距離矩陣大約 400ms就可以算完,再進入VRP的演算。(這裡不考慮使用曼哈頓距離以加速計算) 但是以前文提到一輛3.5頓的堅達一天送100個地址,那麼這個距離矩陣就會有 9,900個最短路徑距離要計算,就要花掉9900x20ms=198秒,才能進入VRP的演算。 光計算距離矩陣就要花掉3分多鐘,更遑論進入複雜的VRP模型找答案了。
其實Google maps有提供一個API就在做距離矩陣運算的,但這個成本非常高,以官網的報價來看,基本定價是一對起訖的最短距離計算要價0.01美金。
以上表的規模,計算距離矩陣要花費20×0.01=2美金,如果你對這個數字沒感覺, 以3.5頓堅達的100個地址來看,就要花9900×0.01=99美金?!然後還不能幫你做最佳路線計算!你要自己寫出可以解算VRP的程式!!
想了解更多資訊?